Definition of a Quadratic Equation
A quadratic
equation is a second-degree polynomial equation in the form:
ax2
+ bx + c = 0
where:
a,b,
and care constants (with a ≠ 0),
x
represents the variable.
Quadratic
equations are fundamental in algebra and appear in various real-life
applications, such as physics, engineering, and finance.
How to
Solve Quadratic Equations
There
are several methods to solve quadratic equations, including:
1.
Factoring Method
If a
quadratic equation can be factored into two binomials, we can set each factor
equal to zero to find the values of x.
2.
Quadratic Formula
The
quadratic formula provides a direct way to find the roots of any quadratic
equation:
It
determines the nature of the roots:
- If b2 − 4ac > 0, there are
two distinct real roots.
- If b2 − 4ac = 0, there is one
real root (a repeated root).
- If b2 − 4ac < 0, there are
two complex (imaginary) roots.
3.
Completing the Square
This
method involves rewriting the quadratic equation in the form (x − p)2
= q and then solving for x by taking the square root on both sides.
4.
Graphical Method
By
plotting the quadratic equation as y = ax2+ bx +c, the solutions
correspond to the points where the graph intersects the x-axis.
Example
Problems
Example
1: Solving
by Factoring
Solve x2
− 5x + 6 = 0.
Solution:
1. Factor
the quadratic equation: (x + p)(x + q) = 0
p + q = -5 and pq = 6
Obtaine the value p = -2 and q = -3
Then (x − 2)(x − 3) = 0
2. Set
each factor to zero: x − 2 = 0 or x − 3 = 0.
3. Solve
for x: x = 2 or x = 3
Thus,
the solutions are x1 = 2 or x2 = 3.
Example
2: Solving
by Factoring
Solve x2
+ 5x − 14 = 0.
Solution:
1. Factor
the quadratic equation: (x + p)(x + q) = 0
p + q = 5 and pq = -14
Obtaine the value p = -2 and q = 7
Then (x − 2)(x + 7) = 0
2. Set
each factor to zero: x − 2 = 0 or x + 7 = 0.
3. Solve
for x: x = 2 or x = -7
Thus,
the solutions are x1 = 2 or x2 = -7.
Example
3: Solving Using the Quadratic Formula
Solve x2
− 6x + 2 = 0 using the quadratic formula.
Solution:
1. Identify
coefficients: a = 1, b = −6, c = 2.
2. Compute
the discriminant: b2 − 4ac = (−6)2 − 4(1)(2) = 36 - 8 = 28
3. Apply the quadratic formula:
Example
4: Solving Using the Quadratic Formula
Solve 2x2
− 4x − 3 = 0 using the quadratic formula.
Solution:
1. Identify
coefficients: a = 2, b = −4, c = -5.
2. Compute
the discriminant: b2 − 4ac = (−4)2 − 4(2)(−3) = 16 + 24 =
40
3. Apply the quadratic formula:
Conclusion
Quadratic
equations can be solved using multiple methods depending on the situation.
Factoring is efficient when possible, the quadratic formula is reliable for all
cases, and completing the square provides insight into the equation's
structure. Mastering these techniques is essential for success in algebra and
beyond.

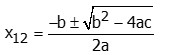


Tidak ada komentar:
Posting Komentar