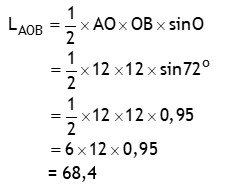TRIGONOMETRI : Cara Menghitung Luas Segitiga Dengan Aturan Sinus

Kali ini kita akan membahas cara menghitung luas segitiga dengan aturan sinus (Trigonometri). Kadangkala suatu segitiga hanya diketahui sisi-sisinya atau kedu sisi dan sudut yang diapitnya. Memang banyak cara mengitung luas segitiga. Salah satunya adalah dengan membagi dua antara perkalian alas dan tinggi.

 

Namun kali ini kita akan membahas luas segitiga menggunakan aturan sinus (trigonometri).

Perhaikan segitiga berikut ini.

Luas segitiga ABC dirumuskan sebagai berikut.

Untuk lebih jelasnya perhatikan beberapa contoh soal dan pembahasan tentang luas segitiga menggunakan aturan sinus berikut ini.

 

Permasalahan 1

Perhatikan segitiga ABC berikut.

Tentukan luas segitiga ABC.

Jawaban:

Sisi yang mengapit sudut A adalah sisi AB dan AC.

Sehingga luas segitiga ABC dengan aturan sinus (trigonometri) sebagai berikut.

Permasalahan 2

Perhatikan segitiga KLM berikut.

Tentukan luas segitiga KLM.

Jawaban:

Sisi yang mengapit sudut M adalah sisi KM dan LM.

Sehingga luas segitiga KLM dengan aturan sinus (trigonometri) sebagai berikut.

Permasalahan 3

Perhatikan segitiga PQR berikut.

Tentukan luas segitiga PQR.

Jawaban:

Sisi yang mengapit sudut Q adalah sisi QR dan PQ.

Sehingga luas segitiga PQR dengan aturan sinus (trigonometri) sebagai berikut.

Permasalahan 4

Perhatikan segi lima beraturan ABCDE berikut.

Tentukan luas segi lima ABCDE.

Jawaban:

Sudut dalam (sudut pusat) pada segi lima ABCDE adalah 360^o : 5 = 72^o.

Sehingga dapat digambarkan sebagai berikut.

Sisi yang mengapit sudut O adalah sisi AO dan OB.

Sehingga luas segitiga AOB dengan aturan sinus (trigonometri) sebagai berikut.

Luas segi lima ABCDE adalah 5 × L_AOB.

Luas ABCDE    = 5 × 68,4

                     = 342

Jadi, luas segi lima ABCDE adalah 342 cm².

 

 

Permasalahan 5.

Perhatikan segi  enam beraturan ABCDEF berikut.

Tentukan luas segi enam ABCDEF.

Jawaban:

Sudut dalam (sudut pusat) pada segi enam ABCDEF adalah 360^o : 6 = 60^o.

Sehingga dapat digambarkan sebagai berikut.

Sisi yang mengapit sudut O adalah sisi AO dan OB.

Sehingga luas segitiga AOB dengan aturan sinus (trigonometri) sebagai berikut.

Demikianlah sekilas materi tentang cara menghitung luas segitiga menggunakan Aturan Sinus (Trigonometri).

Semoga Bermanfaat.

KUMPULAN SOAL CERITA LUAS DAN KELILING BANGUN DATAR (SOAL STANDAR UJIAN SEKOLAH DAN UJIAN NASIONAL)

Dalam kesempatan ini akan kami bahas tentang Keliling dan Luas Bangun Datar. Khususnya yang akan dibahas di sini  adalah soal cerita keliling dan luas bangun datar. Banyak sekali penerapan keliling dan luas bangun datar dalam kehidupan sehari-hari. Oleh karena itu sangat penting kita bahas beberapa contoh soal dan pembahasan tentang soal cerita keliling dan luas bangun datar.

Tujuan pambahasan soal cerita keliling dan luas bangun datar ini agar siswa-siswi dapat menerapkan ilmu tentang bangun datar. Salah satunya mampu mennggunakan materi keliling dan luas bangun datar untuk menyelesaikan masalah.

 

Nah, langsung saja kita akan membahas 10 soal cerita berkaitan dengan keliling dan luas bangun datar.

 

Soal 1

Pak Hanif memagar kebunnya yang berbentuk trapesium. Jarak antara dua pagar yang sejajar adalah 50 m. Jika panjang kebun yang dipagar sejajar masing-masing 80 m dan 100 m. Tentukan luas kebun Pak Hanif.

Jawab:

Panjang sisi sejajar a dan b.

Jarak sisi yang sejajar adalah t.

Luas trapesium

= 1/2 × (a + b) × t

= 1/2 × (80 + 100) × 50

= 1/2 × 180 × 50

= 90 × 50

= 4.500

Jadi, luas kebun Pak Hanif 4.500 m².

  

Soal 2

Di kamar Indra terdapat hiasan dinding yang berbentuk belah ketupat. Panjang        diagonalnya masing-masing 40 cm dan 36 cm. Berapakah luas hiasan dinding tersebut ?

Jawaban:

Panjang diagonal 1 = d₁ = 40 cm.

Panjang diagonal 2 = d₂ = 36 cm.

Luas belah ketupat

= 1/2 × d₁ × d₂

= 1/2 × 40 × 36

= 20 × 36

= 7.200

Jadi, luas hiasan dinding 7.200 cm².

 

Soal 3

Ikhsan membuat layang-layang dari seutas benang, selembar kertas, dan dua batang bambu tipis yang panjangnya 90 cm dan 1 m. berapa meter persegi sekurang-kurangnya kertas yang diperlukan untuk membuat layang-layang?

Jawaban:

Batang bambu yang digunakan untuk membuat layang-layang sebagai diagonal.

Panjang diagonal 1 = d₁ = 90 cm.

Panjang diagonal 2 = d₂ = 1 m = 100 cm.

Luas layang-layang

= 1/2 × d₁ × d₂

= 1/2 × 90 × 100

= 45 × 100

= 4.500

Jadi, luas layang-layang adalah 4.500 cm².

 

Soal 4

Sebuah lapangan berbentuk persegi panjang berukuran 120 m x 80 m. Jika Andi berlari mengelilingi lapangan sebanyak 5 kali, berapa km jarak yang ditempuh Andi.

Jawaban:

Ukuran panjang = p = 120 m

Ukuran lebar = l = 80 m

Lapangan berbentuk persegi panjang.

Keliling = 2 × (p + l)

           = 2 × (120 + 80)

           = 2 × 200

           = 400 m

Jarak tempuh lima kali putaran

= 5 × 400 m

= 2.000 m

= 2 km

Jadi, jarak yang ditempuh Andi adalah 2 km.

 

Soal 5

Kebun ayah berbentuk jajargenjang dengan ukuran panjang sisinya (pagar yang mengelilingi) adalah 40 m dan lebar 25 m. Pagar di sekeliling kebun akan diperbaiki dengan biaya Rp 15.000 per meter. Tentukan biaya yang dibutuhkan ayah untuk memperbaiki pagar seluruhnya.

Jawaban:

Kebun berbentuk berbentuk jajargenjang dengan a = 40 m dan b = 25.

Keliling = 2 × (a + b)

           = 2 × (40 + 25)

           = 2 × 65

           = 130 m

Biaya perbaikan pagar

= 130 × Rp15.000,00

= 1.950.000,00

Jadi, biaya yang dibutuhkan ayah untuk memperbaiki pagar seluruhnya adalah 1.950.000,00.

 

Soal 6

Faiz akan membuat layang-layang untuk dijual. Satu buah layang-layang dibutuhkan dua potong lidi yang digunakan sebagai kerangka dengan panjang masing-masing 30 cm dan 24 cm. Tentukan luas minimal kertas yang dibutuhkan untuk membuat 40 layang-layang.

Jawaban:

Layang-layang mempunyai ukuran diagonal 1 = d₁ = 30 cm dan diagonal 2 = d₂ = 24 cm.

Luas sebuah layang-layang

= 1/2 × d₁ × d₂

= 1/2 × 30 × 24

= 15 × 24

= 360 cm²

Luas kertas untuk membuat 40 layang-layang

= 40 × 360

= 14.400 cm²

= 1,44 m²

Jadi, luas kertas mimimal untuk membuat 40 layang-layang adalah 1,44 m².

 

Nah, untuk soal berikutnya, coba digunakan untuk latihan.

Silahkan mencoba.

Soal 7

Ayah mempunyai sebidang tanah berukuran 45 m x 25 m. Di tanah tersebut akan dibuat sebuah kolam ikan berbentuk belah ketupat dengan panjang diagonal berturut-turut 5 m dan 20 m. Sisa tanah akan ditanami pohon mangga. Berapa meter persegi luas tanah yang ditanami pohon mangga?

 

Soal 8

Diketahui bentuk atap sebuah rumah terdiri atas sepasang trapesium sama kaki dan sepasang segitiga sama kaki. Pada atap yang berbentuk trapesium, panjang sisi sejajarnya masing-masing 50 m dan 30 m. Adapun pada atap yang berbentuk segitiga, panjang alasnya 20 m. Tinggi trapesium sama dengan tinggi segitiga, yaitu 10 m. Jika tiap 1 m² diperlukan 5 buah genteng, tentukan banyak genteng yang dibutuhkan untuk menutup atap tersebut.

 

Soal 9

Sebuah taman dengan bentuk persegi panjang memiliki panjang 48 m dan lebar 32 m. Jika di sekeliling taman akan  dipasang lampu dengan jarak 4 m. Berapa jumlah lampu yang diperlukan?

 

Soal 10

Anita akan membuat pigura berbentuk persegi panjang dengan perbandingan panjang : lebar = 5 : 4. Lebar pigura tersebut 12 cm dan seluruh permukaannya akan ditutupi kertas kado. Berapakah luas kertas kado yang dibutuhkan untuk menutupi seluruh permukaan pigura tersebut?

 

Soal 11

Lantai kelas berbentuk persegi panjang dengan ukuran panjang 12 meter dan lebar 8 meter. Lantai kelas tersebut akan dikeramik dengan biaya Rp50.000,00 per meter persegi. Hitunglah seluruh biaya yang diperlukan untuk memasang keramik di ruang tersebut.

 

 

Demikianlah materi tentang soal standar ujian sekolah dan ujian nasional tentang luas bangun datar.

Semoga bermanfaat.

 

KUMPULAN SOAL STANDAR UJIAN NASIONAL DAN UJIAN SEKOLAH (KESETARAAN ANTARSATUAN WAKTU)

 

Satuan waktu adalah salah satu materi matematika yang diajarkan pada saat sekolah dasar (SD). Karena pentingnya tentang waktu, maka siswa SD/MI paling tidak sudah diperkenalkan tentang waktu. Baik itu secara dasar maupun pada operasi hitung waktu (Kesetaraan antarsatuan waktu).

 

Apa itu satuan waktu?

Waktu adalah berapa lama berlangsungnya suatu peristiwa. Paling mudah mempelajari waktu adalah istilah "lama" dan "sebentar" . Sementara satuan waktu adalah besaran yang digunakan untuk mengukur hasil pengukuran lamanya waktu. Satuan waktu yang biasa dikenal dan dipergunakan dalam kehidupan sehari-hari adalah detik, menit, jam, hari, tahun, dan dekade.

 

 

Jenis Satuan Waktu

Jenis satuan waktu yang biasa dikenal terbagi dalam 2 macam, yaitu:

1. Satuan waktu tak baku

Contoh: ketukan jari, tepuk tangan, ketukan, dan hentakan kaki.

 

2. Satuan waktu yang baku

Contoh: detik, menit, jam, hari, minggu, semester, tahun, dekade, dan abad.

Perhatikan kesetaraan antarsatuan waktu berikut.

1 menit = 60 detik

1 jam = 60 menit

1 jam = 3.600 detik

1 hari = 24 jam

1 pekan = 7 hari

1 bulan = 4 pekan

1 bulan = 28/29/30/31 hari

1 tahun = 12 bulan

1 tahun = 52 pekan

1 tahun = 365 atau 366 hari

1 semester = 6 bulan

1 tahun = 2 semester

1 windu = 8 tahun

1 dekade atau dasawarsa = 10 tahun

1 abad = 100 tahun

1 abad = 10 dekade

 

Bagaimana cara menghitung kesetaraan antarsatuan waktu.

Simak beberapa contoh soal dan pembahasannya berikut ini.

 

1.  5 bulan + 2 minggu + 4 hari =  . . . .

A.  128 hari

B.  136 hari

C.  142 hari

D.  168 hari

Kunci jawaban: D

5 bulan + 2 minggu + 4 hari =  . . .

= 5 × 30 hari + 2 × 7 hari + 4 hari

= 150 hari + 14 hari + 4 hari

= 168 hari

 

2.  3 dasawarsa + 2 windu - 4 tahun = … tahun

A.   1 tahun

B.   26 tahun

C.   42 tahun

D.   46 tahun

Kunci jawaban: C

3 dasawarsa + 2 windu - 4 tahun

= 3 × 10 tahun + 2 × 8 tahun - 4 tahun

= 30 tahun + 16 tahun - 4 tahun

= 42 tahun

 

3.  2 jam - 35 menit + 120 detik = …

A.   85 menit

B.   87 menit

C.   92 menit

D.   98 menit

Kunci jawaban: B

2 jam - 35 menit + 120 detik

= 2 × 60 menit - 35 menit + (120 : 60) menit

= 120 menit - 35 menit + 2 menit

= 87 menit

 

4. 4,5 abad - 7 windu + 5 tahun = …

A.   4.426 tahun

B.   4.439 tahun

C.   4.441 tahun

D.   4.449 tahun

Kunci jawaban: D

4,5 abad - 7 windu + 5 tahun

= 4,5 × 100 tahun  - 7 × 8 tahun + 5 tahun

=  4.500 tahun  - 56 tahun + 5 tahun

= 4.449 tahun

 

5. 4 tahun + 2 semester - 5 bulan = …

A.   55 bulan

B.   56 bulan

C.   65 bulan

D.   70 bulan

Kunci jawaban: A

4 tahun + 2 semester - 5 bulan

=  4 × 12 bulan + 2 × 6 bulan - 5 bulan

=  48 bulan + 12 bulan - 5 bulan

=  55 bulan

 

6. Dian belajar di sekolah dari pukul 07.00 dan berakhir pukul 12.45. Jika selama belajar ia beristirahat 20 menit, maka Elsa belajar selama… menit.

A.   4 jam 45 menit

B.   5 jam 20 menit

C.   5 jam 25 menit

D.   5 jam 30 menit

Kunci jawaban: C.

Lama waktu disekolah

= 12.45 - 07.00

= 5.45

= 5 jam 45 menit

Lama belajar di sekolah

= 5 jam 45 menit - 20 menit

= 5 jam 25 menit

 

 

7. 4,5 bulan - 3 minggu + 5 hari = …

A.   117 hari

B.   119 hari

C.   123 hari

D.   125 hari

Kunci jawaban: B

4,5 bulan - 3 minggu + 5 hari

=  4,5 × 30 hari - 3 × 7 hari - 5 hari

=  135 hari - 21 hari + 5 hari

=  119 hari

 

8. 1,5 jam + 24 menit - 360 detik = …

A.   128 menit

B.   118 menit

C.   112 menit

D.   108 menit

Kunci jawaban: D

1,5 jam + 24 menit - 360 detik

=  1,5 × 60 menit  + 24 menit - (360 : 60) menit

=  90 menit  + 24 menit - 6 menit

=  108 menit

 

8.   3 jam 47 menit 24 detik

      2 jam 29 menit 47 detik +

      …………………………………..

A.   6 jam 16 menit 21 detik

B.   6 jam 17 menit 11 detik

C.   6 jam 17 menit 12 detik

D.   6 jam 18 menit 11 detik

Kunci jawaban: B

      3 jam 47 menit 24 detik

      2 jam 29 menit 47 detik +

      5 jam 76 menit 71 detik

=   5 jam + (1 jam 16 menit ) + (1 menit 11 detik)

=   (5 jam + 1 jam) + (16 menit + 1 menit) + 11 detik

=  6 jam 17 menit 11 detik

 

10. Jika 2 jam yang lalu adalah pukul 09.20. Pukul berapa 1 jam 30 menit kemudian?

A.  Pukul 11.40.

B.  Pukul 11.50.

C.  Pukul 12.40.

D.  Pukul 12.50.

Kunci jawaban: D.

2 jam yang lalu adalah pukul 09.20.

Berarti sekarang pukul (09.20 + 02.00) atau pukul 11.20.

1 jam 30 menit setelah pukul 11.20 adalah pukul (11.20 + 01.30) atau pukul 12.50.

 

 

Bagaimana, sudah paham tentang kesetaraan antarsatuan waktu.

Demikianlah materi tentang kesetaraan waktu dan operasi hitungnya.

Semoga bermanfaat. 

Aturan Kosinus Untuk Menyelesaikan Masalah

 

Jika dalam segitiga hanya mempunyai dua panjang sisi dan mengapit sudut yang besarnya diketahui, maka dapat dicari panjang sisi di depan sudut tersebut.

Atau jika diketahui ketiga sisi pada segitiga, kita dapat menentukan besar sudut pada segitiga tersebut. Untuk mencari unsur-unsur tersebut, kita gunakan aturan kosinus.

 

Aturan Kosinus

Diketahui segitiga ABC dengan panjang sisi-sisinya a, b, dan c. Maka hubungan perbandingan trigonometri antara panjang sisi-sisi segitiga dengan sudut dalam segitiga sebagai berikut.

atau Jika mencari panjang sisi-sisi segitiga menggunakan rumus aturan kosinus berikut..

Untuk lebih jelasnya perhatikan beberapa contoh perhitungan Aturan Kosinus berikut.

Jawaban

Untuk menentukan keliling segi lima beraturan, maka perlu menentukan panjang sisi-sisinya terlebih dahulu.

Misalnya kita akan menentukan panjang AB. Sudut pusat setiap segitiga = 360^o : 5 = 72^o.

Jawaban

Untuk menentukan keliling segi lima beraturan, maka perlu menentukan panjang sisi-sisinya terlebih dahulu.

Misalnya kita akan menentukan panjang AB. Sudut pusat setiap segitiga = 360^o : 8 = 45^o.

Perhatikan Segitiga OAB berikut.

Demikianlah sekilas materi tentang  Aturan Kosinus yang kami sampaikan.

Semoga bermanfaat.

TRIGONOMETRI : Aturan Sinus dalam Segitiga

 

Dalam trigonometri juga dipelajari tentang Aturan Sinus dan Aturan Kosinus (Sine Rule Formula and Cosine RuleFormula).

Apa manfaat Aturan Sinus dan Kosinus dalam segitiga? Coba kalian simak beberapa permasalahan yang muncul di seputar segitiga berikut.

1.   Diketahui segitiga sembarang dengan panjang sisi-sisinya 4 cm, 5 cm, dan 8 cm. Tentukan besar setiap sudut dalam segitiga tersebut.

2.  Diketahui segitiga PQR memiliki sudut P = 30^o, sudut Q = 45^o dan sudut R = 105^o. Jika panjang sisi QR = 12 cm, tentukan panjang sisi PQ dan PR.

3.   Diketahui segitiga sembarang ABC dengan panjang AB = 6 cm dan AC = 8 cm. Sudut yang diapit kedua sisi tersebut adalah 30^o. Tentukan panjang sisi yang ketiga.

 

Itulah beberapa hal yang berkaitan dengan segitiga. Permasalahan di atas dapat diselesaikan dengan menggunakan Aturan Sinus dan Aturan Kosinus (Sine Rule Formula and Cosine RuleFormula). Bagaimana cara menggunakan rumus Aturan Sinus dan Aturan Kosinus?

Memang benar bahwa ketika terdapat permasalahan yang berkaitan dengan segitiga, dan tidak bisa dipecahkan secara sederhana, maka solusinya adalah menggunakan trigonometri. Sekarang marilah mempelajari Aturan Sinus dan Aturan Kosinus.

 

Pada kesempatan ini akan kita bahas Aturan Sinus terlebih dahulu.

Aturan sinus ini banyak manfaatnya dalam kehidupan sehari-hari. Misalnya untuk menentukan jarak dua tempat, Menghitung panjang kawat yang melintas, dan lain sebagainya.

Aturan Sinus

Diketahui segitiga ABC dengan panjang sisi-sisinya a, b, dan c. Maka hubungan perbandingan trigonomometri dengan panjang sisi-sisinya sebagai berikut.

Perhatikan beberapa contoh penerapan aturan sinus berikut.

Panjang QR = 24 cm

Untuk mencari keliling PQR, langkah pertama harus menentukan panjang sisi-sisinya terlebih dahulu. Jadi, panjang PQ dan PR harus ditentukan terlebih dahulu.

Keliling segitiga PQR

K = PQ + QR + PR

   = 33,816 + 24 + 36,053

   = 93,869

Jadi, keliling segitiga PQR adalah 93,869 cm.

 

Demikianlah sekilas materi tentang Aturan Sinus yang dapat kami sampaikan.

Semoga Bermanfaat.